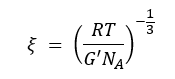Understanding the Importance of Mesh Size of Hydrogels

Knowing the details about the network structure of hydrogels is essential for predicting how they will behave mechanically and biologically in cell culture. One key factor is the mesh size of the hydrogel, which can be compared to the sizes of the molecules that need to move through it. Ideally, the mesh size should be larger than the hydrodynamic radii of these molecules to allow them to diffuse effectively. Therefore, the structure of the hydrogel plays a significant role in determining its suitability and performance in experimental applications.

Challenges in Current Models for Hydrogel Mesh Size

Today, we use quantitative models to link function and structure of hydrogel systems. These models help explain trends seen in experiments and offer general insights into complex interactions that might be tough to understand from just one experiment. However, some of the well-known models that link hydrogel structure with physical properties can be impractical for many hydrogel formulations. For example, the Flory-Rehner equation [1] assumes certain types of networks that may not be present in all hydrogels.

To keep things simple and practical, we focus on a widely-used method [2-5] to determine mesh size known as the Elastic Blob Theory [6]. This theory links data from rheology, specifically the storage modulus, to the mesh size in hydrogels. Simply put, stronger gels with higher crosslink density have smaller mesh sizes.

Applying Elastic Blob Theory to Determine Hydrogel Mesh Size

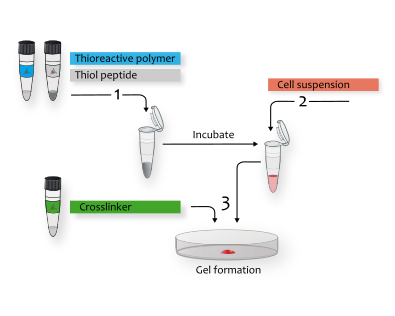
3-D Life Hydrogels are made up of a network of macromolecular chains that exhibit true elastic behavior. This elastic nature allows us to study the network structure using the rubber elasticity theory. Like natural rubber, when a hydrogel undergoes a small deformation, it quickly returns to its original shape. This behavior helps approximate the molecular porosity of the gel.

The mesh size of the hydrogel can be calculated using the storage moduli of swollen gels, as shown in the following equation:

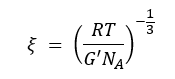
• ξ:Mesh size of the hydrogel.
• R:Gas constant, 8.314 m³ Pa K^-1 mol^-1.
• T:Temperature in Kelvin (for example, 298 K for 25°C).
• G’:Storage modulus, usually given in Pascals (Pa).
• N_A:Avogadro constant, 6.022 × 10²³ mol^-1.

Using this equation, you can estimate mesh sizes ranging from 7 to 34 nanometer for 3-D Life Hydrogels with storage moduli between 10 kPa and 100 Pa.

How to Estimate Mesh Size

To estimate the mesh size of a specific hydrogel, simply find its storage modulus and enter it in the equation together with the temperature to calculate the mesh size. This straightforward approach provides a reliable estimate of a gel's porosity. Keep in mind that the storage moduli provided for 3-D Life Hydrogels correspond to gels before swelling in culture medium.

Literature

1. Flory PJ, Rehner J. Statistical Mechanics of Cross‐Linked Polymer Networks II.  The Journal of Chemical Physics 11, 521–526 (1943).
2. Laaser EJ, Millstone EJ, Simon CZ, Moncure JP. The relationship between gel mesh and particle size in determining nanoparticle diffusion in hydrogel nanocomposites. The Journal of Physical Chemistry B, 2022 Jun 9;126(22):4132-4142.
3. Peppas AN, Richbourg RN. The swollen polymer network hypothesis: Quantitative models of hydrogel swelling, stiffness, and solute transport. Progress in Polymer Science. Volume 105, June 2020, 101243.
4. Werner C, Freundenberg U, Zschoche S, Grimmer M, Zieris A, Prokoph S, Welzel BP. Modulating Biofunctional starPEG Heparin Hydrogels by Varying Size and Ratio of the Constituents. Polymers. 2011, 3(1), 602-620.
5. Kellomäki M, Jönkkäri I, Calejo TM, Ihalainen OT, Karvinen J. Characterization of the microstructure of hydrazone crosslinked polysaccharide-based hydrogels through rheological and diffusion studies. Materials Science and Engineering: C. Volume 94, 1 January 2019, Pages 1056-1066.
6. Shibayama M, Li X, Tsuji Y. Evaluation of Mesh Size in Model Polymer Networks Consisting of Tetra-Arm and Linear Poly(ethylene glycol)s. Gels. 2018 Jun; 4(2): 50.